Author: Joonhee Lim
Date: 2022/07/25
논문 원문: https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=9037111
Neural RRT*: Learning-Based Optimal Path Planning
Rapidly random-exploring tree (RRT) and its variants are very popular due to their ability to quickly and efficiently explore the state space. However, they suffer sensitivity to the initial solution and slow convergence to the optimal solution, which mean
ieeexplore.ieee.org
참고한 글: https://pasus.tistory.com/74?category=1179984
0. Abstract
RRT와 그 변형 모델들은 상태 공간을 빠르고 효율적으로 탐색하는 능력으로 인해 매우 인기가 있다. 그러나 초기 솔루션(초기 샘플링 점)에 민감하고 최적 솔루션에 대한 수렴 속도가 느려 최적의 경로를 찾는 데 많은 메모리와 시간이 소모된다. 자율주행 자동차와 같은 애플리케이션에서는 짧은 경로를 빠르게 찾는 것이 매우 중요하다. 이러한 한계를 극복하기 위해 컨볼루션 신경망(CNN), 즉 NRRT*를 기반으로 하는 새로운 최적 경로 계획 알고리듬을 제안한다. NRRT*는 CNN 모델에서 생성된 불균일한 샘플링 분포를 활용한다. 모델은 다수의 성공적인 경로 계획 사례를 사용하여 훈련된다. 이 논문에서는 A* 알고리즘을 사용하여 지도 정보와 최적 경로로 구성된 훈련 데이터 세트를 생성한다. 계획된 경로의 time cost 및 메모리 사용은 NRRT의 효과와 효율성을 입증하기 위한 지표로 선택된다. 시뮬레이션 결과는 NRRT*가 최첨단 경로 계획 알고리듬과 비교하여 설득력 있는 성능을 달성할 수 있음을 보여준다.
1. Introduction
A* 및 D*를 포함한 그리드 기반 알고리즘은 최적 경로가 존재할 경우 이를 찾을 수 있음을 보장할 수 있다. 그러나 시간 비용과 메모리 사용은 지도 크기와 상태 공간의 차원에 따라 기하급수적으로 증가한다. PRM 및 RRT와 같은 샘플링 기반 알고리즘은 고차원적이고 다중 제약 경로 계획 문제를 효율적으로 해결할 수 있다. 샘플링 기반 알고리즘은 확률적 완전성만 을 제공하고 생성된 경로는 종종 최적이지 않다. 샘플링 기반 플래너의 성능을 결정하는 데 필수적인 요소는 샘플링 분포이다. 왜냐하면 모든 샘플링 기반 플래너는 주어진 샘플링 분포에서 추출한 샘플을 연결하기 위해 반복적으로 트리를 구성하기 때문이다. 일반적으로 Planner는 확률적으로 또는 결정적으로 균일한 분포에서 랜덤 상태 표본을 추출한다. 이러한 샘플링 전략은 확률론적 완전성과 점근적 최적성을 보장할 수 있다. 학습하는데 사용되는 A* 알고리즘은 항상 최적의 경로를 제공하기 때문에 수렴 속도를 크게 높일 수 있다. 다만, 검색 과정에서 사용되는 지도 크기나 단계 크기가 커질수록 A* 알고리즘은 최적의 경로를 찾는 데 훨씬 더 많은 시간과 메모리가 소모된다. 앞서 언급한 한계를 극복하고 A* 및 RRT* 알고리듬을 더욱 활용하기 위해, 본 논문에서는 A* 알고리듬으로부터 학습을 통한 새로운 최적 경로 계획 알고리듬을 제안한다. 우리는 A* 알고리듬에서 생성된 많은 최적 경로를 학습하여 CNN 모델을 훈련시킨다. 새로운 경로 계획 문제가 주어지면, 우리의 훈련된 모델은 RRT* 플래너의 샘플링 프로세스를 안내하는 데 사용되는 최적 경로의 예측 확률 분포를 신속하게 제공할 수 있다.
A. Related Works
A*-RRT*
Thete*-RRT*
2D 가우스 혼합 모델
동적 도메인 RRT
IRRT*
VIN
CVAE
B. Original Contribution
이전 연구와 달리, 우리의 방법론은 인간이 설계한 휴리스틱을 제안하지 않거나 상태 공간의 이산화를 요구하지 않는다. 또한 속성이 다른 최적 경로의 확률 분포를 학습하고 다른 샘플링 기반 알고리듬과 쉽게 결합하여 알고리듬 성능을 더욱 향상시킬 수 있다.
2. Preliminaries
Rapidly-exploring Random Tree는 샘플링 기반 경로계획법이다. 샘플링 기반 경로 계획이란 형상공간을 격자로 분할하지 않고, 랜덤하게 샘플점을 여러 개 생성하여 점점이 공간을 탐색하여 경로를 찾아내는 방법이다. 샘플점을 무작위로 발생시킨 다음 샘플 점 or 두 샘플 점을 잇는 선이 장애물과 충돌하는 지 확인하여 공간의 구조를 파악한다. 랜덤 탐색은 격자생성 방식으로는 탐색이 불가능한 고차원 공간에서 강력한 힘을 발휘한다.
RRT는 공간에서 랜덤하게 샘플 점을 발생시킨 후 트리에서 가장 가까운 노드를 찾는다.
그 두점을 직선으로 연결한 선상에 트리로부터 미리 설정한 거리만큼 떨어진 새로운 점을 트리로 편입한다. 만약 새로운 노드와 기존 노드를 연결한 직선, 즉 트리의 연결선(branch)이 장애물과 충돌한다면 새로운 샘플점을 랜덤하게 다시 발생시킨 후 같은 방법을 다시 시도한다. 이런 방법을 시작점에서 시작하여 목표점이 트리에 연결될 때 반복 시행하면서 트리를 확장시켜서 나가는데, 트리가 고차원의 형상공간 속으로 신속하고 균일하게 확장되면서 자유공간을 효과적으로 탐색하게 된다.
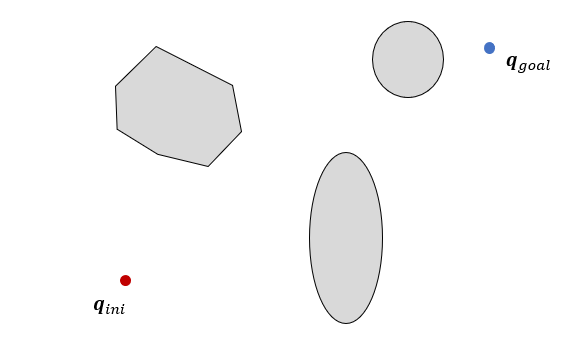

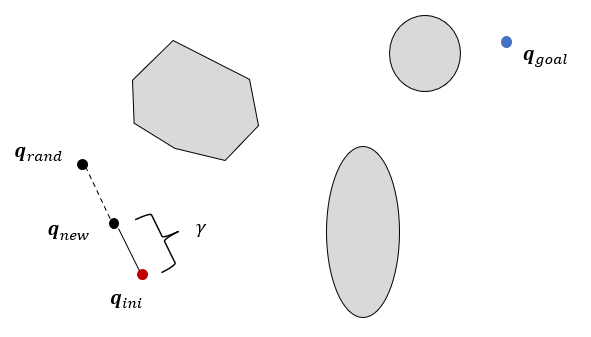
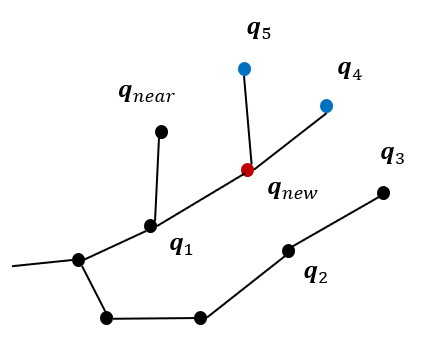
RRT*는 RRT와 2가지 차이점이 있는데 첫 째는 부모 노드의 재선정이고 둘 째는 트리의 재구성이다.
1) RRT*에서는 새로운 노드를 중심으로 일정 반경에 있는 노드들을 뽑고 그 노드들의 cost 비교를 통해 가장 적은 비용을 가진 노드를 부모로 선정한다.
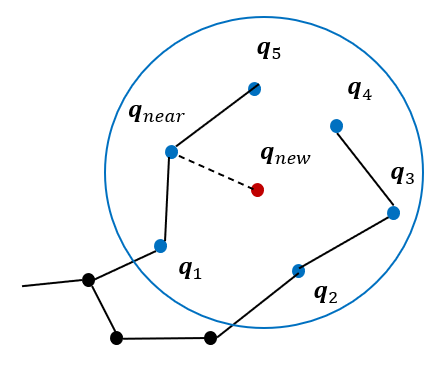

2) 트리의 재구성에서는 새로운 노드를 중심으로 일정 반경에 있는 노드들의 비용과 그 노드들이 새로운 노드의 자식 노드로 연결되었을 때의 비용을 비교하여 자식 노드로 연결되었을 때의 비용이 더 작다면 기존 부모 노드와의 연결을 끊고 새로운 노드의 자식 노드로 연결하여 트리를 재구성한다.
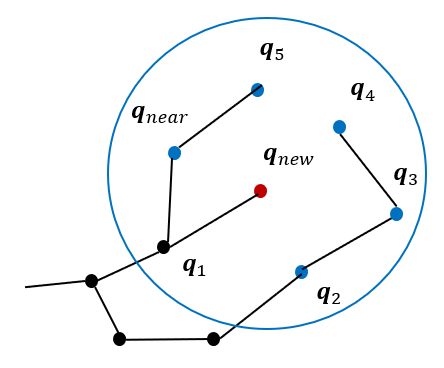
3. NRRT* Algorithm

A. CNN Model
시작지점과 도착지점이 포함된 이미지와 로봇의 Step Size 및 Clearance를 Input으로 하고 CNN와 FCN을 통해 Concatenation한다. 백본 Network로는 ResNet50을 사용하며
C1의 Dimension은 (W/8, H/8, 256)
C2의 Dimension은 (W/32, H/32, 2048)
F1의 Dimension은 (1,1,32) -> (W/8, H/8, 32)
F2의 Dimension은 (1,1,64) -> (W/32, H/32, 64)
더해서 나온게(W/8, H/8, 256 + 32)(W/32, H/32, 2048 + 64) 이곳에 ASPP 적용하면 (W/32, H/32, 256 + 64)
최종적으로
(W/8, H/8, 256 + 32)
(W/32, H/32, 256 + 64) -> (W/8, H/8, 256 + 64)
두 개를 더하면
Final Encoding: (W/8, H/8, 608)
Upconvolution하면Output: (W, H, 1)
B. Loss Function
Loss Function은 각 픽셀 별 Cross-Entropy(Ground Truth와 모델 아웃풋)와 Cross-Entropy(Input과 R?)으로 구성된다.

C. Neural RRT*

NRRT*에서 훈련된 신경망 모델은 처음에 샘플링 프로세스를 초기화하는 데 사용된다. 이 모델은 현재 맵에 대한 최적 경로의 상당히 날카로운 확률 분포를 출력한다. 이 확률분포를 직접 사용하면 완전성 확률은 거의 보장되지 않는다. 따라서 NRRT*에는 두 가지 샘플러가 있는데, 이는 신경망 모델의 불균일한 샘플러와 균일한 샘플러이다. 우리는 균일하게 샘플링할 확률을 α 불균일하게 샘플링할 확률을 (1-α)으로 나타낸다. 많은 시뮬레이션을 통해, 우리는 α = 0.5가 환경의 전체 커버리지를 보장하는 것과 학습된 샘플 영역을 활용하는 것 사이의 최상의 균형을 제공한다는 것을 발견했다. 일반적으로 불균일한 샘플러는 몇 개의 샘플로 실현 가능한 경로를 빠르게 찾을 수 있다. 그러나 불균일 샘플러가 용액 영역을 완전히 식별하지 못하면 균일 샘플러가 효과적으로 공백을 메워야 한다. 즉, 불균일 샘플러가 이러한 영역을 찾을 수 있도록 더 많은 샘플이 필요하다. 우리는 예측된 샘플링 분포 O의 상태 값이 편광된다는 것을 발견했다. 즉, 예측된 최적 경로에 위치한 상태 값이 1에 근접하는 반면 다른 상태의 값은 0에 근접한다. 따라서 불균일한 샘플링 과정에서 0.5 미만의 값은 사용하지 않는다. NRRT*와 RRT*의 차이점은 다른 샘플링 기반 알고리즘에서 쉽게 사용할 수 있는 샘플링 기법이라는 점이다.
D. Probabilistic Completeness and Asymptotic Optimality
NRRT*에서 불균일 샘플러는 확률 1 - α로 상태를 샘플링하는 반면, 균일 샘플러는 확률 α로 샘플링한다. 반복 횟수가 무한대로 증가함에 따라 상태 공간의 각 상태가 샘플링된다는 의미이기에 확률론적 완전성은 자연스럽게 보장된다.
RRT* 알고리즘의 점근적 최적성에 대한 이론적 보장은 다음 방정식이 성립할 경우 성립한다.
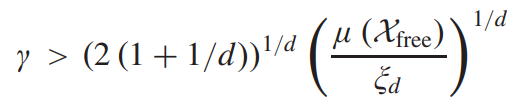
γ는 search radius
d는 dimensionality
μ(Xfree)는 Lebesgue measuer of Xfree
ξd는 Volume of unit ball in the d-dimensional Euclidean space
동일한 과정이 RRT*에서 발생하므로 NRRT*도 점근적 최적이라고 볼 수 있다.
4. Simulation Results
A. Training Details
최적화: Adam(β1 = 0.9 and β2 = 0.999)
학습률: 0.0001
Batch Size: 20
제안된 신경망은 지도 크기, 간격 또는 Step Size에 관계없이 최적 경로의 예측 확률 분포를 출력하는 데 50ms밖에 걸리지 않는다. -> 휴리스틱 경로를 찾기 위해 A* 알고리즘을 사용하는 것에 비해 많은 시간 비용을 절약한다.
- 5576개의 서로 다른 2-D 랜덤 맵을 사용
- 각 지도의 크기: 201 × 201 Pixel
- c1은 Clearance: 1이고 s1은 Step Size: 1이라는 의미
무작위로 12개의 다른 시작 및 목표 상태를 설정하며 훈련 데이터 셋은 1070592개의 이미지
우리는 최적의 경로를 찾기 위해 A* 알고리즘을 사용한다.
B. Path Planning Under Different Clearance
이 섹션에서는 서로 다른 간격에서 경로 계획 문제에 대한 세 가지 알고리즘의 성능을 테스트한다.
- 테스트하는 간극의 종류: 1, 2, 4, 6(간극이 크면 계획된 경로가 장애물과 멀리 떨어져 있음을 의미하며, 간극이 작으면 계획된 경로가 장애물에 가깝다는 것을 의미한다.)
- 신경망에 대한 Step Size의 입력: 2
RRT* 및 IRRT*의 경우 간격은 사전 정의된 파라미터지만 NRRT*에서 신경망 모델은 다른 간격 설정에 따라 불균일 샘플러를 공급하기 위해 해당 샘플링 분포를 출력한다.

그림 4(a)~(h)는 서로 다른 간격 설정 하에서 서로 다른 두 지도에 대한 예측 샘플링 분포를 나타낸다. 빨간색과 녹색 사각형은 각각 시작 상태와 목표 상태를 나타냅니다. 자홍색은 해당 영역이 최적 경로를 포함할 수 있는 더 높은 가능성을 가지고 있음을 나타내고, 파란색은 더 낮은 가능성을 나타낸다. 최적 경로는 예측된 확률 분포에 있음을 알 수 있다. 따라서, 신경망의 예측을 불균일한 샘플러로 사용하여, NRRT*는 초기 솔루션을 빠르게 찾고 최적의 솔루션으로 수렴할 수 있다. 다만 일부 예측 결과가 완벽하지 않다는 지적이 나온다. 예를 들어, 그림 4(b) 및 (f)에서는 최적 솔루션이 위치할 수 없는 일부 영역을 예측 결과의 일부로 간주한다. 그림 4(c), (f), (g)에서 예측된 샘플링 영역은 연속적이지 않다. 하지만 시뮬레이션을 통해 이러한 불완전한 예측이 성능에 거의 영향을 미치지 않는다는 것을 발견했다. 그 이유는 RRT 알고리즘이 전체 상태 공간을 탐색할 수 있는 능력을 가지고 있기 때문이다.(불균일 샘플러와 균일 샘플러를 둘 다 사용하기 때문) 덧붙여 그림 4(b), (c), (f), (g)로부터 특히 클리어런스 설정에 따라 예측이 많이 변화함을 알 수 있다. 그 이유는 최적의 경로가 실제로 다른 간격 설정에서 변경되기 때문이다.
평가지표:
- 시간: GPU가 CNN을 실행하기 위해 사용되기 때문에 경로 계획 과정에서 CPU 시간 비용과 GPU 시간 비용의 합계
- 노드: 최적의 솔루션을 찾을 때 노드의 수.

1) NRRT*는 최적의 경로를 찾기 위해 최소 시간 비용과 노드를 사용한다. 이는 NRRT*가 RRT* 및 IRRT*에 비해 많은 계산 자원을 절약할 수 있다는 것을 의미한다.
2) NRRT*의 시간 비용 및 노드의 표준 편차가 훨씬 작으며, 이는 더 나은 안정성을 나타낸다.
3) 간격이 변경됨에 따라 RRT*와 IRRT*는 최적의 경로를 찾기 위해 서로 다른 시간 비용과 노드를 필요로 한다. 그러나 NRRT*에 사용된 시간 비용과 노드는 많이 변경되지 않으며, 이는 NRRT*의 양호한 견고성을 보여준다.
C. Path Planning Under Different Step Size
이번에는 다른 Step size로 경로 계획에 대한 세 가지 알고리듬의 성능을 테스트한다.
- 테스트하는 Step Size(A* 알고리즘의 검색 범위, 예를 들어, 2단계는 A* 플래너가 각 방향에서 두 개의 그리드를 검색): 1, 2, 4, 6
- 간극 입력: 1
A* 알고리즘의 단계 크기 설정에 따라 최적의 경로가 달라진다.
학습 데이터 셋에 사용된 최적 경로가 A* 알고리즘에서 나온 것이기 때문에 NRRT*는 Step Size에 민감하다.
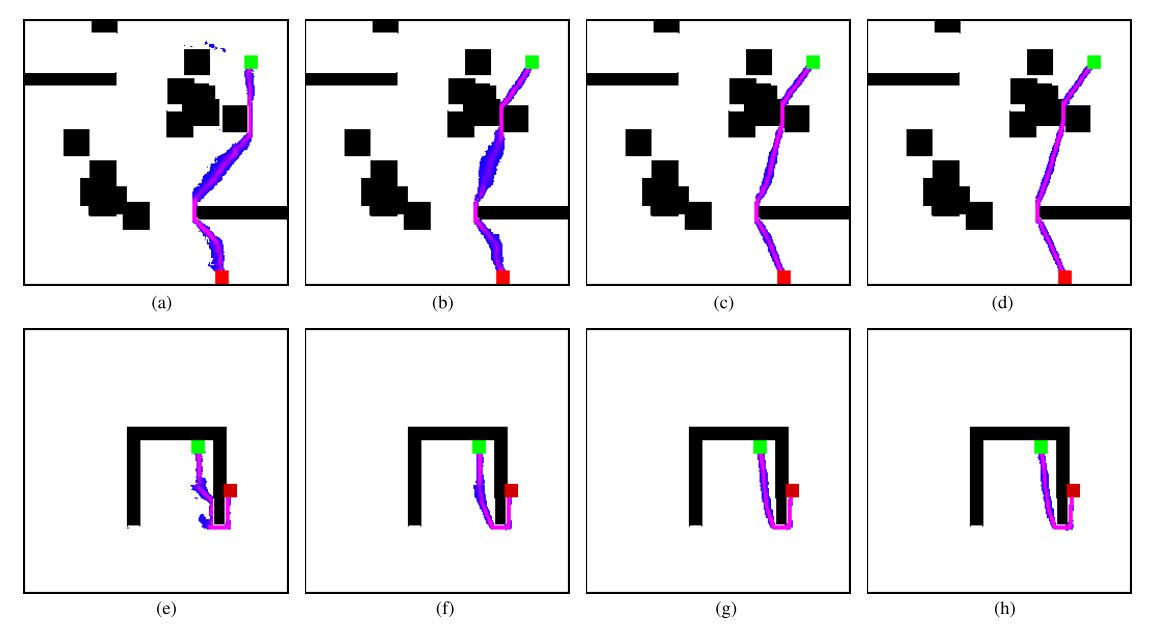
그림 6(a)-(h)는 서로 다른 Step Size에서 두 지도(맵 3, 4)의 예측 표본 분포의 그림을 보여준다. Step Size가 작은 값으로 설정되면 큰 값에 비해 최종 경로가 최적이 아니다. 그러나 Step Size를 큰 값으로 설정하면 A* 알고리즘의 시간 비용이 기하급수적으로 증가한다. 그러나 NRRT*는 항상 다른 Step Size에서 샘플링 분포를 빠르게 예측한다.
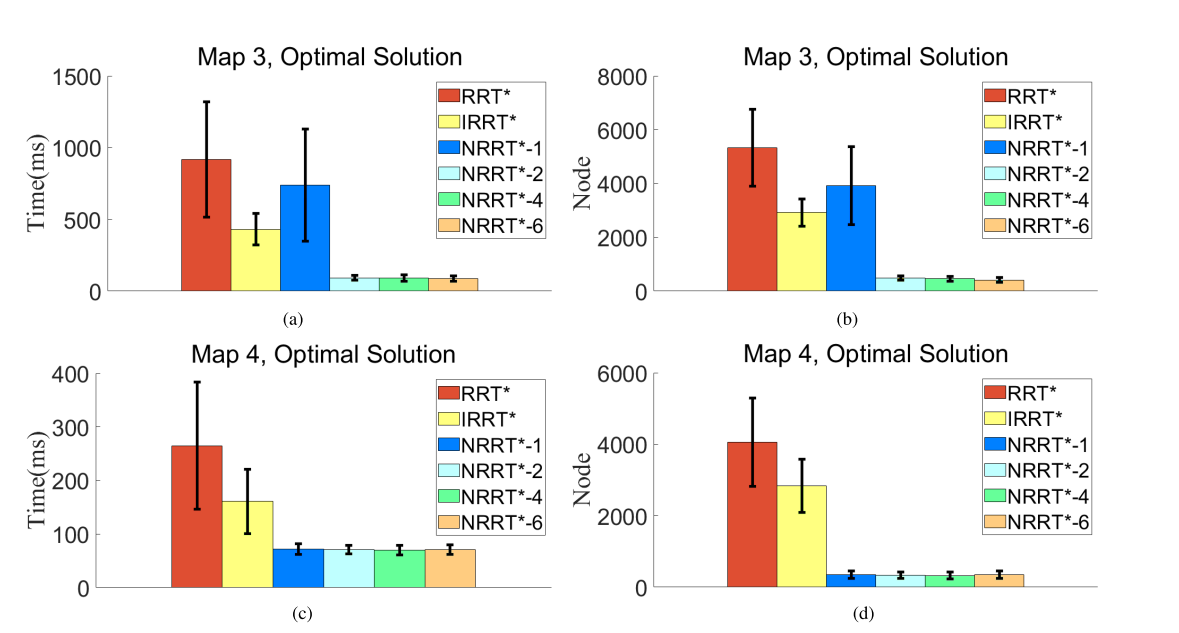
상이한 단계 크기 설정에서의 시뮬레이션 결과는 다음과 같다. 그림 6(a)–(d)의 경우, 생성된 초기 경로가 이미 최적 경로에 매우 가깝기 때문에 NRRT*-2, NRRT*-4 및 NRRT*-6은 최적 경로를 찾기 위해 훨씬 적은 시간 비용과 노드를 사용한다. 그러나 NRRT*-1의 예측 샘플링 분포는 최적 경로를 포함하지 않기 때문에 크게 도움이 되지 않았다. 이는 A* 알고리즘을 사용하여 휴리스틱 경로를 찾는 알고리즘의 큰 한계이기도 하며 Step Size가 크면 전처리에 많은 시간이 소요되지만 Step Size가 작으면 좋은 휴리스틱 경로를 보장할 수 없다. 그러나 NRRT*에서는 추가 시간 비용 없이 좋은 휴리스틱 경로를 보장하기 위해 더 큰 단계 크기를 설정할 수 있다. 요약하자면, NRRT*는 각기 다른 Step Size 설정에서 다시 설득력 있는 성능을 달성하였다.
5. Conclusion and Future Work
CNN 모델과 RRT* 알고리듬을 기반으로 A* 알고리듬에서 성공적인 계획 사례의 양을 학습하여 Path Planning 과정에서 최적 경로쪽으로 불균일한 샘플링을 하기 위해 NRRT*를 제안한다. 경로 계획에서 서로 다른 제약 조건을 충족하기 위해, 간격과 단계 크기가 모두 설계된 CNN 모델에서 고려되었다. 시뮬레이션 결과는 제안된 알고리듬이 기존 알고리듬에 비해 훨씬 더 우수한 성능을 발휘한다는 것을 보여줍니다. 제안된 알고리듬은 새로운 샘플링 기법이며, 개선된 결과를 위해 다른 샘플링 기반 알고리듬에 쉽게 적용할 수 있다는 장점이 있다. 또한 미래에 확장가능한 다양한 시나리오가 존재한다.
1) 의미 인식 경로 계획(Task를 이해하고 인간과 상호작용하는?)
2) Raw 포인트 클라우드 데이터를 사용하여 운동역학 제약 조건을 충족하면서 실시간 최적 경로 계획
3) 신경망 모델을 사용하여 사회적으로 호환되는 경로 계획 설계
이미 존재하는 알고리즘을 Learning시켜서(DL, RL) 다른 알고리즘에 가이드라인으로써 사용하면 괜찮은 결과를 낼 수 있는 것 같다.


