Author: Joonhee Lim
Date: 2022/09/07
출처: https://velog.io/@legendre13/Optimal-Frenet-planning-algorithm
https://tonylim.tistory.com/63
0. Motivation
자율주행 Planning에 대해서 공부하던 중 Frenet Frame과 이를 이용한 Planning 알고리즘에 대해 정리해보고자 한다. 해당 Frame은 도로 형상의 방향으로 s-axis 가 도로와 수직방향으로 d-axis가 펼쳐져서 작관적이고 편리하다는 장점이 있다.
1. Frenet Frame Planning Algorithm
1) 좌측은 Cartesian Frame 우측이 Frenet Frame
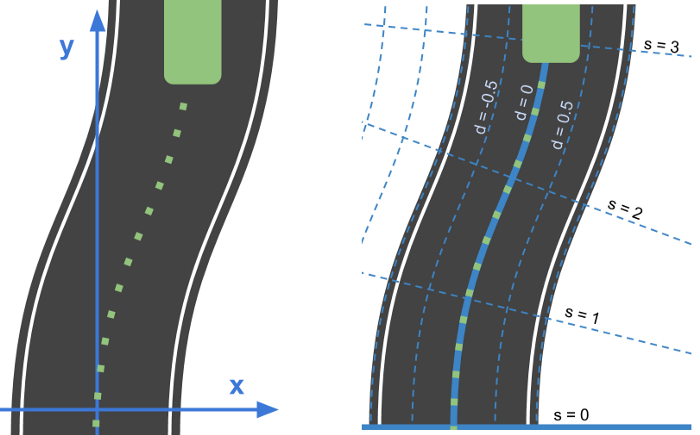
기존의 공간 곡선은 $r(t) = x(t)i+y(t)j+z(t)k$로 나타내지만 이 곡선을 새로운 벡터 T, N, B를 통해 해석할 수도 있다.
이것이 Frenet Frame이다. 정의는 다음과 같다.
주어진 곡선은 모든 점에서 미분가능한 매끄러운 곡선이고 곡률은 0이 아니다.
$$단위 접선벡터: T = dr/ds$$
$$단위 법선벡터: N = {1/k}*{dT/ds}$$
$$단위 이중법선벡터: B = T X N$$
변수 t에 대한 미분으로 곡률과 비틀림을 구하는 공식을 알아두어야 한다.
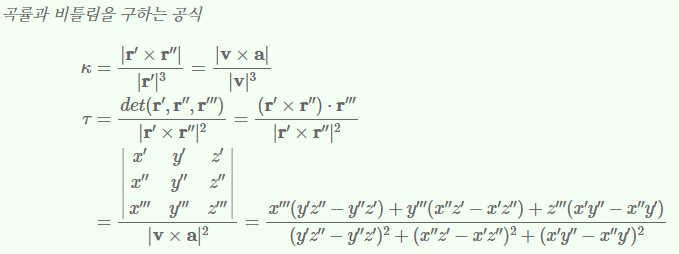
2) Frenet Frame 상에서 Polynomial Path를 생성
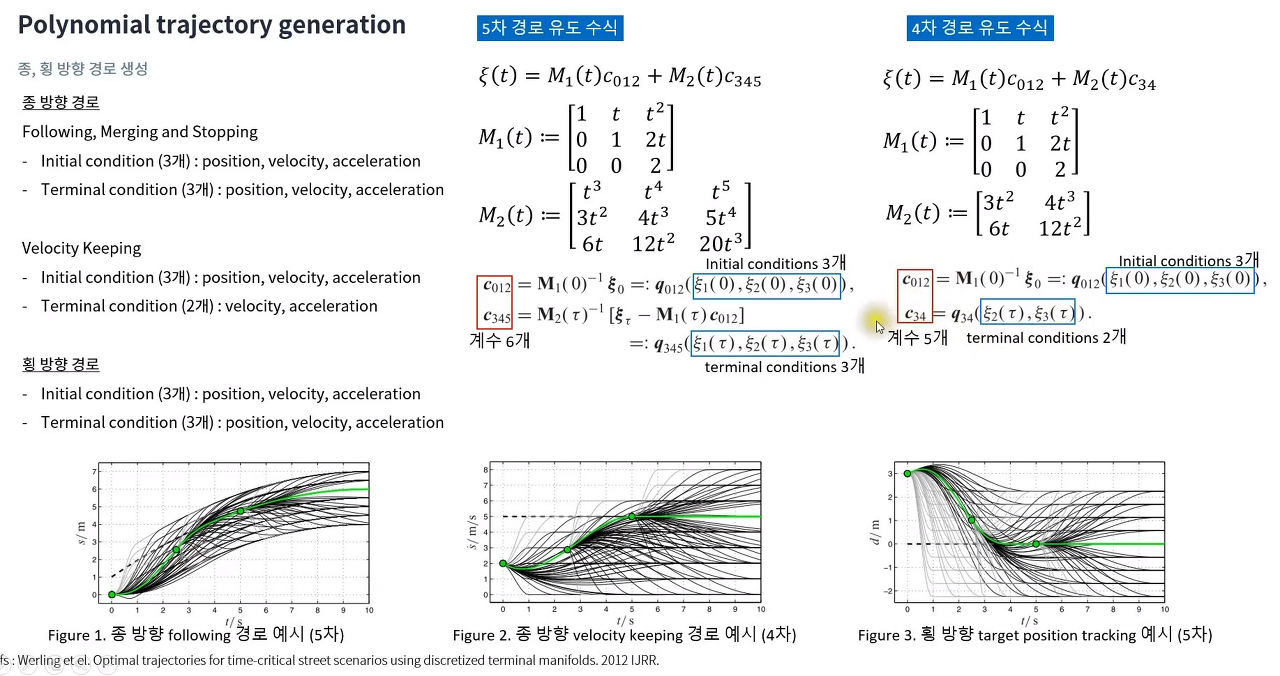
- 횡방향, 종방향 : initial value $x_i, v_i, a_i$와 target value $x_f, v_f, a_f$와 target time T로 5차 다항식 계산
- 속도 유지 : initial value $x_i, v_i, a_i$와 target value $x_f, v_f, a_f$와 target time T로 4차 다항식 계산
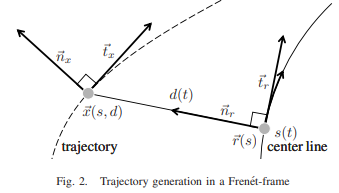
d(t): 중심으로부터 횡거리
$n_r, t_r$: reference path의 법선, 접선벡터
다음과 같이 횡방향, 종방향 각기 다른 경로가 생성되면 이 둘을 합쳐서 진짜 경로를 뽑아낸다.
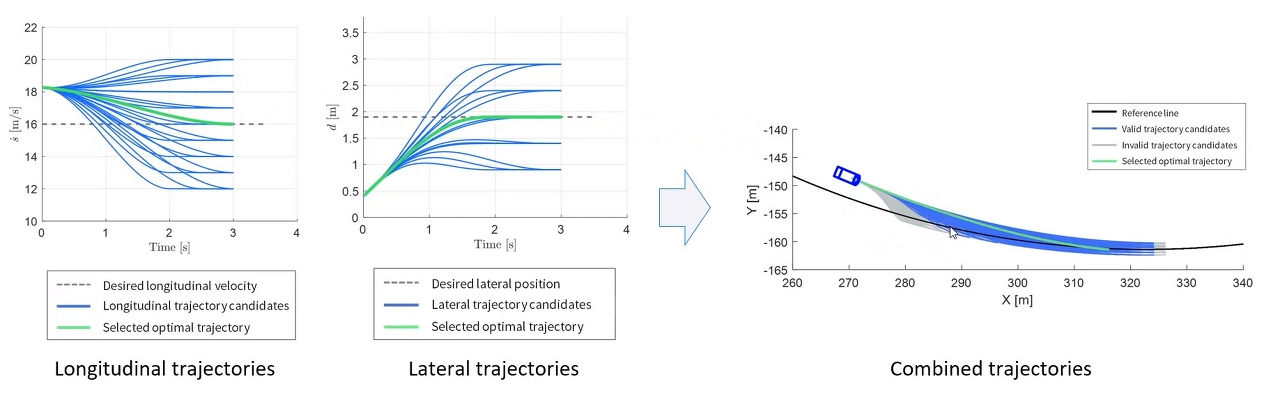
수 많은 경로 중 가장 조건에 알맞은 Trajectory를 선택하면 된다.
3) Trajectory Check
- 속도 제한 체크: $s'(t) <=s'_{limit}$
- 가속도 제한 체크: $s''(t)^2+d''(t)^2 <=a^2_{max}$
- curvature 제한 체크: $k는 [k_{min},k_{max}]$
- collision 체크 : Euclidean distance-based check
4) Optimal Trajectory selection
- 종방향 Cost
- longitudinal jerk : 종 방향 안정감
- veltocity deviation : 타켓 속도와 얼마나 근접하였는지
- time interval : 얼마나 빨리 조건에 도달하였는지

- 횡방향 Cost
- lateral jerk : 횡 방향 안정감
- time interval : 얼마나 빨리 조건에 도달하였는지
- terminal lateral deviation : 이전 optimal 경로와의 변화, 경로 떨림 방짐
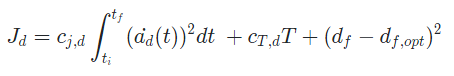
- Total Cost
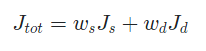
일반적으로 사람들은 횡방향에 더 민감하게 반응하기 때문에 편의를 위해 횡방향 Cost에 Weight를 더 많이 부가하는 편이다.
1) Waypoint들을 Cubic spline Planner로 rx,ry,ryaw, rk(곡률)을 만들어내고
2)
'Autonomous Driving' 카테고리의 다른 글
| [AD] PRM(Probabilistic Road-Map) 알고리즘 설명 (0) | 2022.09.13 |
|---|---|
| [AD] 자율주행 시뮬레이터 비교 (0) | 2022.09.13 |
| [AD] Potential Field Algorithm 설명 (0) | 2022.09.07 |
| [AD] DWA(Dynamic Window Approach) vs TEB(Timed-Elastic-Band) 알고리즘 비교 (0) | 2022.09.07 |
| [AD] D*(Dynamic A*) 알고리즘 설명 (0) | 2022.09.03 |


