Author: Joonhee Lim
Date: 2022/09/02
출처: https://m.blog.naver.com/jjz0426/221135413776
0. Motivation
Model Predictive Control과 같은 경로 추종 알고리즘을 사용하기 위해서는 차량 동역학 모델이 필요하다. 그 중 논문에서 굉장히 많이 보였었던 Bicycle Model에 대해서 알아보고자 이 글을 작성한다. 뭐든지 알고 쓰면 좋지 않겠냐는 마인드다. 보는 Control 논문마다 나오는 것들은 정리해두면 참 유용한 것 같다. (강화학습으로 치면 MDP나 Bellman Equation, Off/On-Policy을 공부하는 느낌이랄까)
1. Why is it called a bicycle model?
아주 재미난 것은 차량 모델인데 이름은 자전거 모델이라는 것이다. 그 이유는 4륜 차량의 각 앞&뒷 바퀴를 하나로 변환하여 역학을 계산하기 때문에 자전거 모델이라고 부른다는 것이다.
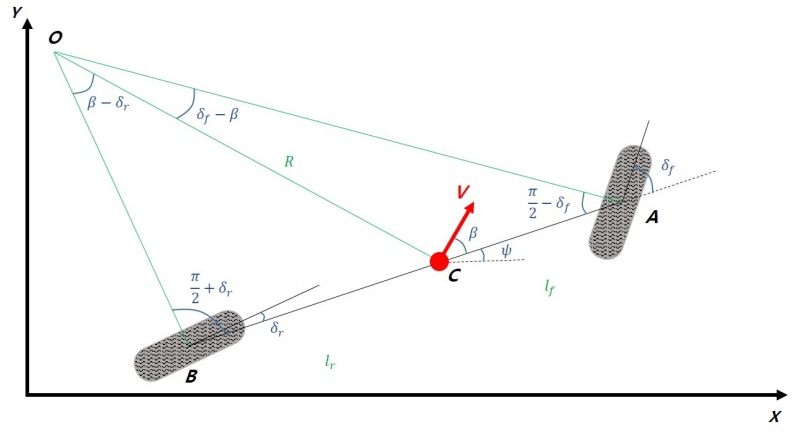
A와 B: 전륜 후륜 중심점
C: 질량 중심
$l_f, l_r$: 질량 중심과 전륜 후륜 중심점까지의 거리
V: 질량 중심점에서 속도벡터
- 매우 중요한 Bicycle Model의 가정
1) 전륜/후룐에서 일어나는 슬립은 없으며 질량 중심 C에서만 슬립이 일어난다.
2) Bicycle Model 자체가 저속에 적합한 모델이므로 5m/s 미만의 저속으로 운동한다(?)
3) Parameter는 다음을 의미한다.
- $\beta$: 슬립 각(slip angle)
- $\psi$: 방향각(Heading angle)
- $\delta_f$: 전륜 Steering angle
- $\delta_r$: 후륜 Steering angle
4) 차량 서스펜션 및 수직 방향 움직임으로부터 발생하는 효과는 무시한다.
5) 지면의 굴곡 및 높이 차이는 없다
- Equations of motion
삼각형 AOC와 BOC에서 각각 사인법칙을 적용하면,

가 되어 두 개의 식을 유도할 수 있다. 두 식을 더하게 되면

다음과 같은 방정식이 도출되는데 Yaw의 시간에 대한 변화량 Yaw rate를 구할 수 있다.
또한 X방향과 Y방향의 속도도 V와 $\psi$와 $\beta$로 표현하면
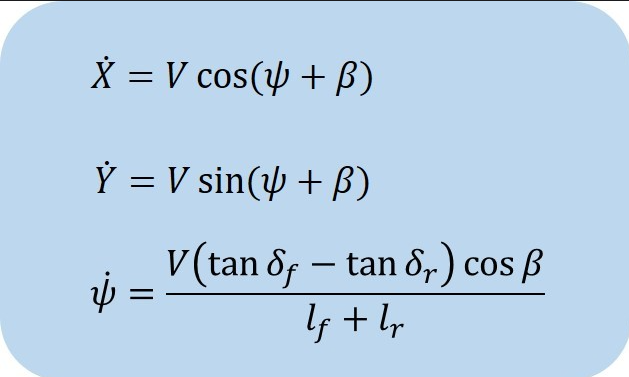
다음과 같은 수식을 구할 수 있다.
- Slip Angle
앞서 구한 두 개의 식으로 슬립각 $\beta$를 구할 수 있다.
2식에 $l_f$을, 1tlrdp $l_r$을 곱하고 아래와 같이 연립방정식을 풀어주면
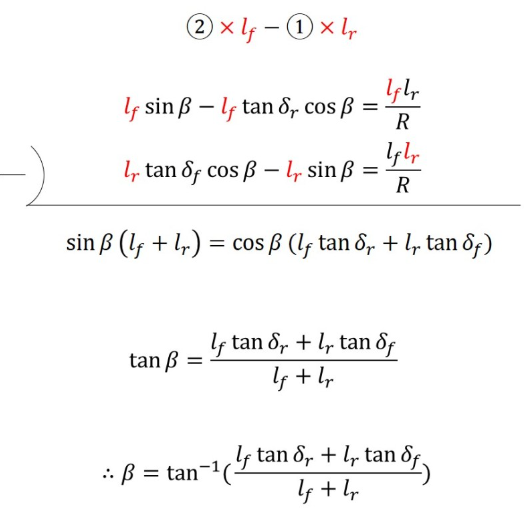
슬립각 $\beta$를 알고 있는 값을 통해 구할 수 있다.
- 실제 차량에서의 운동 방정식 적용
Bicycle Model에는 다양한 변수가 존재하고 또 그 변수들이 변하는 경우까지 고려하여 설계됐지만 실제로는 더 간단한 운동 방정식을 나타낼 수 있다.
1) 실제 차량에서는 일반적으로 후륜은 조향되지 않는다. ($\delta_r=0$)
2) 실제 선회를 하며 주행하기 위해 Steering을 조작하는 상황에서 각도 변화는 굉장히 작은 편이다. (매우 작은 $\delta_r$)
3) 전륜의 조향각이 작아짐에 따라 차량의 길이 방향 직선 AB와 속도 벡터 V가 이루는 각이 작아진다. ($\beta$가 매우 작아짐)
따라서 실제로는 다음과 같다.
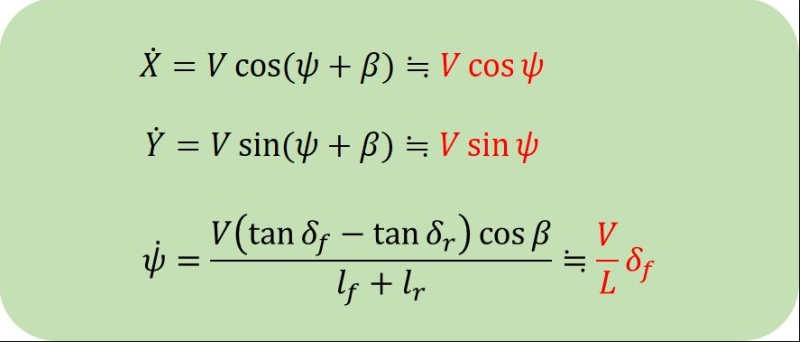
다음과 같이 Bicycle Kinematic Model은 차량의 속도와 Sterring angle을 입력으로 차량의 운동을 나타낼 수 있는 모델이다.
다음 Post에서는 Bicycle Dynamics 모델과 아커만 모델에 대해서 포스팅해야겠다.
'Autonomous Driving' 카테고리의 다른 글
| [AD] Ackermann Kinematic Model 설명 (0) | 2022.09.02 |
|---|---|
| [AD] Bicycle Dynamic Model 설명 (0) | 2022.09.02 |
| [AD] Stanley Tracking Algorithm 설명 (0) | 2022.09.01 |
| [AD] Pure Pursuit Control Tracking Algorithm 설명 (0) | 2022.09.01 |
| [AD] Tracking Controller 성능 비교(MPC, PPC, PID, LQR, Stanley) (0) | 2022.09.01 |



